Resolvendo um exercício de Programação Dinâmica
Em pleno espírito natalino, hoje resolvi fazer algo diferente: escrever um artigo em português :D! Neste post eu vou discutir um problema bastante interessante dado numa das cadeiras da universidade (Desenho e Análise de Algorítimos 20/21).
O problema
Escreva um programa que, dado um conjunto de N números, descubra para cada um deles qual a menor quantidade de dígitos a adicionar a cada um deles para os transformar numa capicua. Uma capicua é um número (ou conjunto de números) cujo reverso é ele próprio. A figura abaixo mostra alguns exemplos de Input e Output esperados para este problema.
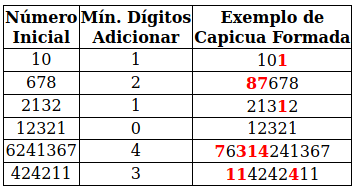
Resolução
A primeira abordagem em qualquer problema de Dynamic Programming é sempre perceber bem o que é pedido (isso é válido não só em DP, mas em qualquer problema). Podemos imaginar que um número pode ser descrito por "aXb", onde a é o primeiro dígito do número e b, o último. Se estivermos a calcular a quantidade de dígitos que temos que adicionar para tornar o número uma capicua usando uma função count(num), então se $a = b$, count(num) = 0 + count(X). Caso contrário, count(num) = 1 + count(X). Como já lidamos com o primeiro e último dígito, faremos a mesma comparação para o número X, este que é um subproblema similar. Note também que a escolha do lado em que iremos adicionar o novo dígito importa: tome como exemplo o número $6241367$. Inicialmente, vamos supor que nosso algorítimo, ao verificar que $a \neq b$, simplesmente adiciona um dígito no final do número e, em sequência, faz a mesma comparação para o número do meio X. Neste caso, teríamos:
1) Inicialmente, comparamos o primeiro dígito com o último: $6 \neq 7$, portanto adicionamos um 6 no final do número, fazendo com que a quantidade de dígitos necessários para transformá-lo numa capicua, até agora, seja total = 1. O número fica portanto $62413676$. Agora, fazemos a mesma coisa para o número “do meio” 241367.
2) Fazemos o mesmo processo para o número 241367. Como $2 \neq 7$, adiciona-se $2$ no final número e ficamos com $2413672$ e com total = 2, pois tivemos que adicionar um dígito ao número.
Já nesse ponto podemos parar e refletir em algo. E se o nosso algorítimo adicionasse um novo dígito não no final do número, mas sim no início dele? Se refizermos o processo, em 1) ficaríamos com $76241367$ (total = 1 da mesma maneira), mas em 2) verificamos que no número 624136 $a = b$ e não precisamos adicionar nenhum dígito ao número. Temos então duas formas pelas quais podemos adicionar dígitos ao número. Qual então seria a melhor forma de ter certeza que estamos usando aquela que adiciona a menor quantidade de dígitos ao número? Bem, devemos simplesmente comparar os dois métodos e usar o método que adiciona… o menor número de digitos! Isso se transmite naturalmente para um código recursivo como veremos a seguir.
Podemos implementar nosso algoritimo trabalhando com o número em formato String. Dessa forma, podemos selecionar a posição de dígitos facilmente com o método do java String.charAt(). Se à primeira posição da string num dermos o nome de l e chamarmos a última posição r, a solução recursiva para esse problema pode ser então desenvolvida:
public static int count(String num, int l, int r){
if(l >= r) return 0;
if(num.charAt(l) == num.charAt(r))
return 0 + count(num,l+1,r-1,c);
else
return 1 + Math.min(count(num,l+1,r), count(num,l,r-1));
}
Entretanto, este algoritimo calcula várias vezes o mesmo valor para cada par $(r,l)$. É possível ver isso na figura abaixo para o número 25234:
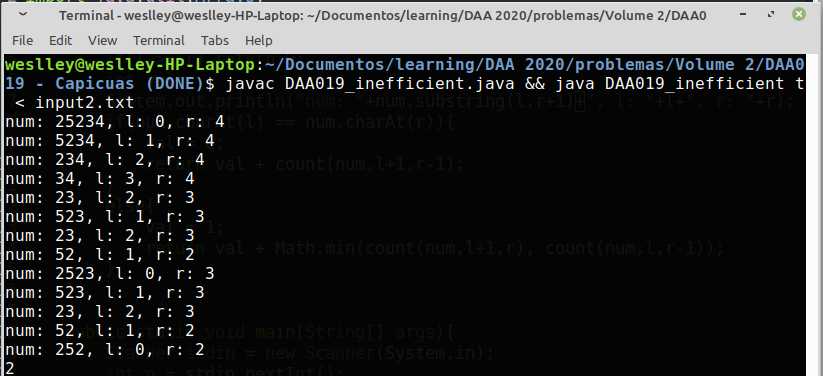
Note que a função calcula o número de dígitos necessários para tornar $52$ capicua 2 vezes (para $23$ são necessárias 3). Quanto maior a quantidade de dígitos do número num, mais ineficiente este algoritimo se torna (é de facto exponencial!).
É aqui que utilizamos Dynamic Programming (juntamente com memoization). O poder dessa técnica está no facto de reutilizar resultados que já foram calculados, tornando o processo muito mais eficiente (complexidade polinomial). Para guardar os resultados de posições $(r, l)$ já calculados, usaremos uma matriz que contém a quantidade de dígitos necessários para tornar o número uma capicua indo da posição l até a posição r. Esse número fica guardado, então, em c[l][r]. Ao utilizarmos isso, nosso algoritimo fica:
public static int count(String num, int l, int r, int[][] c){
if (c[l][r] != -1) return c[l][r];
if(l >= r) return 0;
int ans;
if(num.charAt(l) == num.charAt(r))
ans = 0 + count(num,l+1,r-1,c);
else
ans = 1 + Math.min(count(num,l+1,r,c), count(num,l,r-1,c));
c[l][r] = ans;
return ans;
}
A primeira linha do método count() checa se o resultado que queremos já foi calculado anteriormente. Caso afirmativo, esse resultado é retornado (e o cálculo é feito apenas uma vez). No final, o resultado ans para um dado par $(r, l)$ é salvo na matriz c[l][r]. A imagem a seguir mostra como não são mais feitos cálculos repetidos para pares $(r, l)$ para o número 25234.
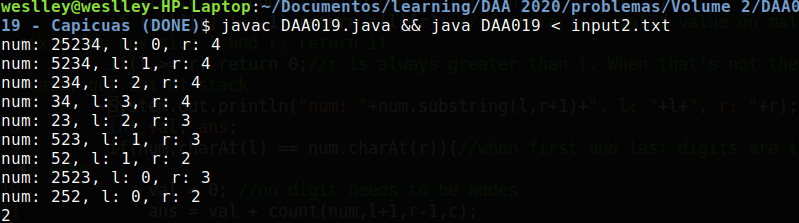
Verifica-se que só é calculado valores para o número 52 e 23 uma vez devido ao facto de que guardamos esses valores para quando, na stack recursiva, eles precisarem serem novamente calculados.
A função main() desse problema, com o método count() acima definido, fica então:
public static void main(String[] args){
Scanner stdin = new Scanner(System.in);
int n = stdin.nextInt();
for(int i=0;i<n;i++){
String num = stdin.next();
int L = num.length();
//matrix that will store number of digits to add to number from position l to r
int[][] c = new int[L][L];
//initializing matrix with unused values
for(int k=0;k<L;k++)
for(int m=0;m<L;m++)
c[k][m] = -1;
System.out.println(count(num,0,L-1,c));
}
}
Com a explicação deste (excelente) exercício é possível ver o motivo pelo qual DP é uma ferramenta bastante útil e versátil na solução de problemas de optimização.